Nolta Simulated Systems Software
AdvDCSM Important Application Examples
Consider the following important and extremely complex Digital Communication Systems/Subsystems examples* that the software system tool AdvDCSM Digital Communication System Simulator [AdvDCSMT1DCSS (T1)] can model and simulate for study or conceptual prototype design:
i) Convolutional or Block Coded or UnCoded Signaling over Discrete-Time Waveform Channels versus Vector Channels can be studied using T1.
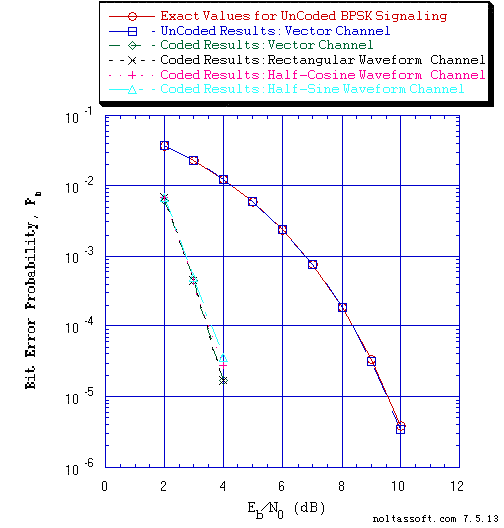
Consider for an example the BER or bit error probability (Pb) performance simulation results of a very important Rate (R) = 1/2, Constraint Length (K) = 7 convolutional code that were produced by T1. They are displayed below in the Figure 1 plot for UnCoded BPSK Signaling over a Vector Channel and Coded BPSK Signaling over Vector and Discrete-Time Waveform Channels.
iii) Convolutional or Block Coded or UnCoded Signaling over Actual Coherent Single AWGN Channels: study the degree of degradation of the Bit Error Rate (BER) caused by the effect of Phase-Lock Loop (PLL) Steady-State Phase Error of a channel;
This problem of Channel Synchronization and Phase Coherency in a Digital Communication System is extremely important and difficult to study.
Consider for an example the Actual Coherency BER or bit error probability (Pb) performance simulation results that were produced by T1. They are displayed below in the Figure 2 plot for UnCoded 16-QAM Signaling and the Figure 3 plot for Convolutional Coded 16-QAM Signaling. Note that the PLL Beta parameter is dependent on the Signal to Noise Ratio (SNR) at the input of the Phase-Lock Loop.
iv) Convolutional or Block Coded or UnCoded Signaling over Non-Ideal/Distorting Single AWGN Channels: study the degree of degradation of the Bit Error Rate (BER) caused by the non-flat Frequency Response of a channel;
v) Block/Symbol Interleaver-DeInterleaver design for Burst Channels;
vi) Diversity-Combiner or Symbol Interleaver-DeInterleaver design for Convolutional or Block Coded Signaling over Fading Channels with Additive White Gaussian Noise (AWGN);
Note that T1, the AdvDCSM system tool contains important Vector and Discrete-Time Waveform Fading Channel models (Rayleigh, Rician and Frequency-Selective). T1 allows for simulations of complex information-theoretic digital communication systems using these Fading Channel models.
vii) Convolutional or Block Coded or UnCoded Signaling over Real-Valued or Complex-Valued InterSymbol Interference (ISI) Channels with AWGN;
viii) Linear Equalization Transversal Filter Design using Minimum Mean-Square-Error (MMSE) Criterion for Real-Valued or Complex-Valued InterSymbol Interference Channels;
These problems of InterSymbol Interference, i.e., the dispersion or smearing of the transmitted channel signal, and the application of Linear Equalizers, i.e., counteract the channel dispersion, in a Digital Communication System are extremely important and difficult to study.
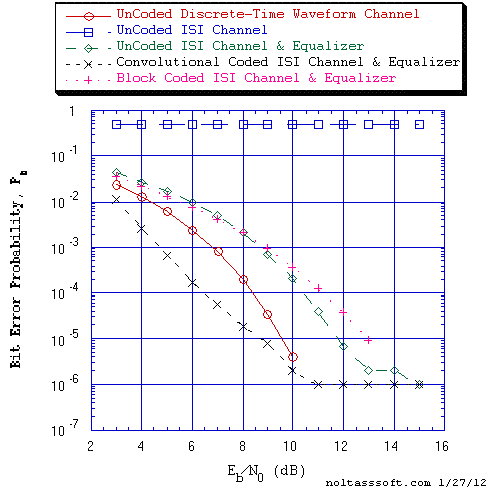
Consider for an example the InterSymbol Interference Bit Error Rate (BER) or Bit Error Probability (Pb) performance simulation results for an equivalent White Noise Discrete-time (DT) ISI Channel model of a data-quality telephone line and Linear Equalizer that were produced by T1. They are displayed below in the Figure 4 plot for UnCoded 2-PAM Signaling, for Convolutional Coded 2-PAM Signaling, and for Block Coded 2-PAM Signaling.
Note that this problem of equalizer coefficients determination belongs to the class of Wiener Filtering problems for Estimation of Discrete-Time Random Processes.
And the Wiener-Hopf Equation for this ISI and MSE Equalizer problem is derived using the Orthogonality Principle and is in the form of a matrix equation that provides an analytical solution to the tap weights determination problem.
Consult Digital Communications by John G. Proakis for a description of this equivalent DT channel of InterSymbol Interference of length ten (10).
ix) Convolutional (Non-Orthogonal or Orthogonal Non-Recursive) or Block Coded or UnCoded Signaling over AWGN Ideal or Non-Ideal Parallel MultiChannels;
x) Convolutional or Block Coded or UnCoded Signaling over Crosstalk Ideal or Non-Ideal Parallel MultiChannels with AWGN: investigate the effect of Crosstalk on Viterbi Algorithm Channel Decoder or Block Code Channel Decoder BER Performance;
xi) Convolutional or Block Coded or UnCoded Discrete MultiTone Modulation (DMT) Signaling over Ideal or Non-Ideal/Distorting Parallel MultiCarriers/MultiChannels with AWGN.
* Note: Consult the "AdvDCSMT1DCSS Key Capabilities and Features" section of this Website to determine the very large set of all possible Digital Communication System/Subsystems cases that can be modeled and simulated using T1.
i) Convolutional or Block Coded or UnCoded Signaling over Discrete-Time Waveform Channels versus Vector Channels can be studied using T1.
Consider for an example the BER or bit error probability (Pb) performance simulation results of a very important Rate (R) = 1/2, Constraint Length (K) = 7 convolutional code that were produced by T1. They are displayed below in the Figure 1 plot for UnCoded BPSK Signaling over a Vector Channel and Coded BPSK Signaling over Vector and Discrete-Time Waveform Channels.
Figure 1. Bit Error Probability for UnCoded and Rate = 1/2 Convolutional Coded BPSK
Signaling over a Coherent Memoryless Channel with Additive White Gaussian
Noise (AWGN):
Rate = 1/2, K = 7, (3, 1, 0, 3, 3, 2, 3) a Best (Optimal) Non-Recursive
Convolutional Code and Viterbi Algorithm Decoder using a Path Memory Length
of 35 bits and Unquantized Branch Metric;
Equal probable IID Source for 10 Million Information Bits for UnCoded BPSK
Signaling over a Vector Channel;
Equal probable IID Source for 1 Million Information Bits for Convolutional
Coded BPSK Signaling over a Vector and Discrete-Time Waveform Channel; &
Discrete-Time Waveform Channel: eight samples per symbol period for
rectangular orthonormal baseband shaping pulse and rectangular matched
filter demodulator; eight samples per symbol period for half-cosine
orthonormal baseband shaping pulse and half-cosine matched filter
demodulator; and eight samples per symbol period for half-sine
orthonormal baseband shaping pulse and half-sine matched filter demodulator.
ii) Binary Source with Memory (Markov Sources), Convolutional Coded Signaling and Optimal Viterbi Algorithm Channel Decoders can be studied using T1's
unique design of a MAP (Maximum A Posteriori Probability) Viterbi Algorithm Decoders for Markov Sources;iii) Convolutional or Block Coded or UnCoded Signaling over Actual Coherent Single AWGN Channels: study the degree of degradation of the Bit Error Rate (BER) caused by the effect of Phase-Lock Loop (PLL) Steady-State Phase Error of a channel;
This problem of Channel Synchronization and Phase Coherency in a Digital Communication System is extremely important and difficult to study.
Consider for an example the Actual Coherency BER or bit error probability (Pb) performance simulation results that were produced by T1. They are displayed below in the Figure 2 plot for UnCoded 16-QAM Signaling and the Figure 3 plot for Convolutional Coded 16-QAM Signaling. Note that the PLL Beta parameter is dependent on the Signal to Noise Ratio (SNR) at the input of the Phase-Lock Loop.
Figure 2. Bit Error Probability for UnCoded Gray coded 16-QAM Signaling over an
Actual Coherent Memoryless Channel with Additive White Gaussian Noise
(AWGN).
Figure 3. Bit Error Probability for Coded Gray coded 16-QAM Signaling over an
Actual Coherent Memoryless Channel with Additive White Gaussian Noise
(AWGN):
r = 1/4, K = 4, {15, 9, 7, 15} Maximal minimum free distance
Non-Recursive Convolutional Code (S. Lin & D.J. Costello) and Viterbi
Algorithm Decoder.
Consult Digital Communications by John G. Proakis for a discussion on the 'Effect of Noise on Phase Estimation.' In this discussion, the 1966 work of A.J. Viterbi on the derivation of the phase error probability density function is presented for the case of the first-order PLL.iv) Convolutional or Block Coded or UnCoded Signaling over Non-Ideal/Distorting Single AWGN Channels: study the degree of degradation of the Bit Error Rate (BER) caused by the non-flat Frequency Response of a channel;
v) Block/Symbol Interleaver-DeInterleaver design for Burst Channels;
vi) Diversity-Combiner or Symbol Interleaver-DeInterleaver design for Convolutional or Block Coded Signaling over Fading Channels with Additive White Gaussian Noise (AWGN);
Note that T1, the AdvDCSM system tool contains important Vector and Discrete-Time Waveform Fading Channel models (Rayleigh, Rician and Frequency-Selective). T1 allows for simulations of complex information-theoretic digital communication systems using these Fading Channel models.
vii) Convolutional or Block Coded or UnCoded Signaling over Real-Valued or Complex-Valued InterSymbol Interference (ISI) Channels with AWGN;
viii) Linear Equalization Transversal Filter Design using Minimum Mean-Square-Error (MMSE) Criterion for Real-Valued or Complex-Valued InterSymbol Interference Channels;
These problems of InterSymbol Interference, i.e., the dispersion or smearing of the transmitted channel signal, and the application of Linear Equalizers, i.e., counteract the channel dispersion, in a Digital Communication System are extremely important and difficult to study.
Consider for an example the InterSymbol Interference Bit Error Rate (BER) or Bit Error Probability (Pb) performance simulation results for an equivalent White Noise Discrete-time (DT) ISI Channel model of a data-quality telephone line and Linear Equalizer that were produced by T1. They are displayed below in the Figure 4 plot for UnCoded 2-PAM Signaling, for Convolutional Coded 2-PAM Signaling, and for Block Coded 2-PAM Signaling.
Figure 4. Bit Error Probability for UnCoded 2-PAM Signaling, Convolutional Coded
2-PAM Signaling, and Block Coded 2-PAM Signaling over an InterSymbol
Interference Channel and Linear MSE Equalizer with Additive White
Gaussian Noise (AWGN):
r = 1/2, K = 5, {3, 2, 2, 1, 3} a Best (Optimal) Non-Recursive
Convolutional Code (J.P. Odenwalder) and Viterbi Algorithm Decoder;
L = 3, N = 6, [3,5,6] Systematic Block Code and Likelihood Block
Decoder;
ISI DT Channel: 11-Tap Gain Coefficients Linear Transversal Filter; &
Linear MSE Equalizer: 31-Tap Weights Linear Transversal Filter.The Minimum Mean-Square-Error (MMSE) Linear Equalizer (Transversal Filter) tap weights (coefficients) are determined by applying the Wiener-Hopf Equation to this particular channel of InterSymbol Interference of finite length ten (10) and 31-Tap Weights Transversal filter case.
Note that this problem of equalizer coefficients determination belongs to the class of Wiener Filtering problems for Estimation of Discrete-Time Random Processes.
And the Wiener-Hopf Equation for this ISI and MSE Equalizer problem is derived using the Orthogonality Principle and is in the form of a matrix equation that provides an analytical solution to the tap weights determination problem.
Consult Digital Communications by John G. Proakis for a description of this equivalent DT channel of InterSymbol Interference of length ten (10).
ix) Convolutional (Non-Orthogonal or Orthogonal Non-Recursive) or Block Coded or UnCoded Signaling over AWGN Ideal or Non-Ideal Parallel MultiChannels;
x) Convolutional or Block Coded or UnCoded Signaling over Crosstalk Ideal or Non-Ideal Parallel MultiChannels with AWGN: investigate the effect of Crosstalk on Viterbi Algorithm Channel Decoder or Block Code Channel Decoder BER Performance;
xi) Convolutional or Block Coded or UnCoded Discrete MultiTone Modulation (DMT) Signaling over Ideal or Non-Ideal/Distorting Parallel MultiCarriers/MultiChannels with AWGN.
* Note: Consult the "AdvDCSMT1DCSS Key Capabilities and Features" section of this Website to determine the very large set of all possible Digital Communication System/Subsystems cases that can be modeled and simulated using T1.
T1 is NOW AVAILABLE as a TRIAL VERSION that will allow you to use T1, a Digital Communication (Information-Theoretic) System Modeling and Simulation software tool, for a Limited Period without Charge and to learn about the valuable utility of T1 in the study, evaluation, and possibly design of certain Complex Digital Communication Systems first hand before purchase.
OR BUY:
BUY T1 (ADVDCSMT1DCSS software system tool)NOW.
OR
BUY T1 Version 2 5G NR LDPC Code R software system tool NOW.
- ORDER AdvDCSM System Tool Product Now
- AdvDCSM System Tool and LOW-DENSITY PARITY-CHECK CODING
- AdvDCSM System Tool and TURBO CODING
- Advanced Turbo Decoding and Iterative Stopping Rule
- Advanced Turbo Coding and Rate Matching
- OBTAIN FREE TRIAL USE of AdvDCSMT1DCSS (DOWNLOAD)
- Nolta Simulated Systems Software Introduction
- Advanced Digital Communication System Modeler (AdvDCSM) Technology
- AdvDCSM Important Application Examples
- AdvDCSM Professional and Advanced Application Examples
- AdvDCSM Key Capabilities and Features
- AdvDCSM Further Product Information
- AdvDCSM Product SUPPORT
- Background on AdvDCSM Development
- Research on Problems of Diffraction, Scattering, and Propagation of Waves
- Addendum to Research on Problems of Diffraction, Scattering, and Propagation of Waves: Diffractive Edge and Singularity
